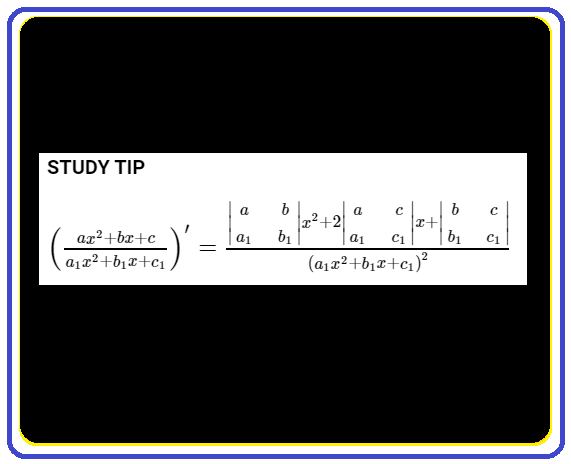
Các bài viết trước đã giới thiệu công thức đạo hàm hay quy tắc đạo hàm. Đó là cơ sở lý thuyết học sinh cần phải hiểu rõ. Để học sinh có thể hiểu sâu và vận dụng thành thạo thì admin giới thiệu bộ bài tập trắc nghiệm đạo hàm. Các bài trắc nghiệm được sắp xếp từ căn bản tới nâng cao với mục tiêu giúp học sinh lĩnh hội kiến thức một cách hiệu quả.
Câu 1. Cho một hàm số có dạng \(y = {\left( {{x^7} + x} \right)^2}\). Hãy tính đạo hàm
A.\(\left( {{x^7} + x} \right)\left( {7{x^6} + 1} \right)\)
B.\(2\left( {7{x^6} + 1} \right)\)
C.\(2\left( {{x^7} + x} \right)\left( {{x^6} + 1} \right)\)
D.\(2\left( {{x^7} + x} \right)\left( {7{x^6} + 1} \right)\)
Hướng dẫn giải
Sử dụng công thức (với \(u = {x^7} + x\) )
\(y’ = 2\left( {{x^7} + x} \right).{\left( {{x^7} + x} \right)^/} = 2\left( {{x^7} + x} \right)\left( {7{x^6} + 1} \right)\)
Câu 2. Giả sử hàm số \(y = {\left( {{x^2} + x + 1} \right)^4}\). Đạo hàm của y(x) nhận kết quả
A.\(4{\left( {{x^2} + x + 1} \right)^3}.\)
B.\({\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
C.\({\left( {{x^2} + x + 1} \right)^3}.\)
D.\(4{\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
Hướng dẫn giải
Sử dụng công thức \({\left( {{u^\alpha }} \right)^/}\)với \(u = {x^2} + x + 1\)
Câu 3. Cho hàm số \(y = {\left( {{x^2} + x + 1} \right)^4}\). Đạo hàm của hàm đó có kết quả
A.\(4{\left( {{x^2} + x + 1} \right)^3}.\)
B.\({\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
C.\({\left( {{x^2} + x + 1} \right)^3}.\)
D.\(4{\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
Hướng dẫn giải
Sử dụng công thức \({\left( {{u^\alpha }} \right)^/}\)với \(u = {x^2} + x + 1\)
\(y’ = 4{\left( {{x^2} + x + 1} \right)^3}.{\left( {{x^2} + x + 1} \right)^/} = 4{\left( {{x^2} + x + 1} \right)^3}.\left( {2x + 1} \right)\)
Câu 4. Hãy tính đạo hàm lượng giác cơ bản sau \(y = x\cos x\) .
A.\(\cos x – \sin x.\)
B.\(x\cos x.\)
C.\(x\sin x.\)
D.\(\cos x – x\sin x.\)
Hướng dẫn giải
Ta áp dụng đạo hàm tích.
\(y’ = x’\cos x + x.{\left( {\cos x} \right)^/} = \cos x – x\sin x.\)
Câu 5: Hãy tính đạo hàm của hàm lượng giác có chứa căn thức\(y = \sin \sqrt x \).
A.\(\frac{1}{{\sqrt x }}.\cos \sqrt x .\)
B.\(\frac{1}{{\sqrt x }}.\cos \sqrt x .\)
C.\(\frac{1}{{\sqrt x }}.\sin \sqrt x .\)
D.\(\frac{1}{{2\sqrt x }}.\cos \sqrt x .\)
Hướng dẫn giải
Áp dụng \({\left( {\sin u} \right)^/},\) với \(u = \sqrt x \)
\(y’ = {\left( {\sin \sqrt x } \right)^/} = \cos \sqrt x .{\left( {\sqrt x } \right)^/} = \frac{1}{{2\sqrt x }}.\cos \sqrt x .\)
Câu 6. Cho hàm số lượng giác \(y = \sqrt {\cos 2x} \). Giá trị của đạo hàm là
A. – \(\frac{{\sin 2x}}{{2\sqrt {\cos 2x} }}.\)
B.\(\frac{{ – \sin x}}{{\sqrt {\cos 2x} }}.\)
C.\(\frac{{\sin 2x}}{{2\sqrt {\cos 2x} }}.\)
D.\(\frac{{ – \sin 2x}}{{\sqrt {\cos 2x} }}.\)
Hướng dẫn giải
Áp dụng \({\left( {\sqrt u } \right)^/},\) với \(u = \cos 2x\)
\(y’ = \frac{{{{\left( {\cos 2x} \right)}^/}}}{{2\sqrt {\cos 2x} }} = \frac{{ – \sin 2x.{{\left( {2x} \right)}^/}}}{{2\sqrt {\cos 2x} }} = \frac{{ – \sin 2x}}{{\sqrt {\cos 2x} }}.\)
Câu 7. Cho $f\left( x \right) = \frac{1}{x} + \frac{2}{{{x^2}}} + \frac{3}{{{x^3}}}$. Tính $f’\left( { – 1} \right)$.
A.-14
B.12
C.13
D.10
Hướng dẫn giải
Bước đầu tiên tính đạo hàm sử dụng công thức ${\left( {\frac{1}{{{x^\alpha }}}} \right)^/} = \frac{{ – \alpha }}{{{x^{\alpha + 1}}}}$
$f’\left( x \right) = {\left( {\frac{1}{x} + \frac{2}{{{x^2}}} + \frac{3}{{{x^3}}}} \right)^/} = – \frac{1}{{{x^2}}} – \frac{4}{{{x^3}}} – \frac{9}{{{x^4}}}$$ \Rightarrow f’\left( 1 \right) = – 1 – 4 – 9 = – 14$
Hy vọng với bài viết khá cẩn thận và các bài tập trắc nghiệm được lọc từ đề thi thử sẽ giúp học sinh học tập hiệu quả hơn. Chúc em học tốt!