Để hiểu thêm về dạng toán cách chứng minh đường thẳng vuông góc với mặt phẳng thì bạn nên xem trước bài góc giữa 2 đường thẳng, khi đó có thể hiểu sâu về dạng toán này
Mục lục
Cơ sở lý thuyết
Để chứng minh đường thẳng vuông góc với mặt phẳng ta cần 3 cách cần phải nhớ:
- Cách 1: Nếu 2 mặt phẳng // với nhau mà 1 đường thẳng khi ⊥ với 1 trong 2 mặt phẳng thì vuông góc với mặt phẳng còn lại $\left\{ \begin{array}{l} \left( \beta \right)//\left( \alpha \right)\\ d \bot \left( \beta \right) \end{array} \right. \to d \bot \left( \alpha \right)$
- Cách 2: Nếu một đường thẳng d đồng thời vuông góc với hai đường thẳng cắt nhau thì d sẽ vuông góc với mặt phẳng chứa 2 đường thẳng cắt nhau đó: $\left\{ {\begin{array}{*{20}{l}} {{d_1} \subset \left( \alpha \right),{d_2} \subset \left( \alpha \right)}\\ {{d_1} \cap {d_2} = Q}\\ {d \bot {d_1}}\\ {d \bot {d_2}} \end{array}} \right. \to d \bot \left( \alpha \right)$
- Cách 3: Nếu 1 đường thẳng Δ bất kì mà vuông góc với 1 mặt phẳng thì khi d song song với Δ thì d chắc chắn sẽ vuông góc với mặt phẳng đó $\left\{ \begin{array}{l} \Delta \bot \left( \alpha \right)\\ d//\Delta \end{array} \right. \to d \bot \left( \alpha \right)$
Bài tập có lời giải
Dựa vào cơ sở lý thuyết trên, ta cùng nhau vào phần bài tập.
Bài tập 1. Một tứ diện ABCD, trong đó mặt phẳng (BCD) có góc C bằng π/2 và AB vuông góc với (BCD). Hãy chứng minh CD vuông góc với mặt phẳng (ABC)
Hướng dẫn giải
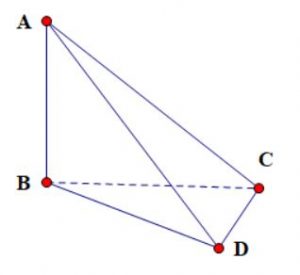
Theo dữ kiện bài ra ta có:
$\begin{array}{l} \widehat C = \frac{\pi }{2} \Rightarrow CD \bot BC\left( 1 \right)\\ AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 2 \right) \end{array}$
Từ (1) và (2) ta suy ra điểu cần chứng minh là CD ⊥ (ABC)
Bài tập 2. Cho một hình chóp MNPQ, hình chóp này có đặc điểm là mặt đáy (MNP) có góc N bằng π/2 và QP luôn vuông góc với (MNP). Hãy chứng minh hai đường thẳng MN và QN vuông góc với nhau.
Hướng dẫn giải
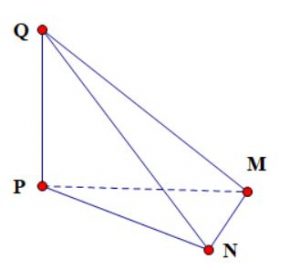
Vì mặt đáy có góc N bằng π/2 => PN ⊥ NM (1)
Theo đề QP ⊥ (PNM) => QP ⊥ MN (2)
Từ (1) và (2) suy ra: NM ⊥ (QPN) => NM ⊥ QN (Điều phải chứng minh)
Bài toán 3. Cho hình chóp có đỉnh E và mặt đáy là (SGQ). Biết rằng ES vuông với (SQG) và $\widehat {SQG} = \frac{\pi }{2}$. Trong mặt phẳng (ESQ), gọi H là hình chiếu của S lên cạnh EQ. Hãy chứng minh rằng QG ⊥ SH.
Hướng dẫn giải
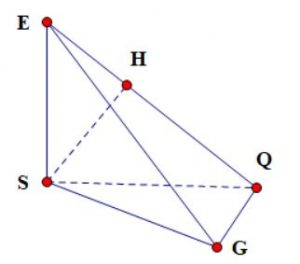
Ta thấy ES ⊥ (SQG) => ES ⊥ QG (1)
Vì mặt phẳng (SQG) có $\widehat Q = \frac{\pi }{2}$ => QS ⊥ QG (2)
Từ (1) và (2) => QG ⊥ (ESQ) (3)
Theo đề, SH thuộc mặt phẳng (ESQ) (4)
Từ (3) và (4) suy ra: QG ⊥ SH (điều cần chứng minh)
Trên là hướng dẫn chi tiết, hy vọng nó hữu ích với bạn.