Để biết cách tính thể tích hình trụ, trước tiên bạn cần nhớ được công thức thể tích hình trụ trước
Mục lục
Cơ sở lý thuyết
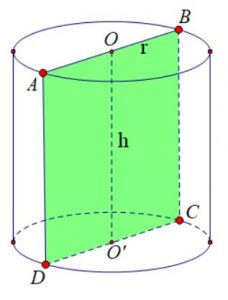
Công thức thể tích khối trụ: $V = h.\pi .{r^2}$
Trong đó:
- Thể tích khối trụ là V ( đơn vị là m3)
- Chiều cao khối trụ hay còn gọi là đường cao là h ( đơn vị m)
- Bán kính mặt đáy là r ( đơn vị là m)
- π = 3,14 là hằng số
Bài tập thể tích có lời giải
Bài toán 1: Một khối trụ có chiều cao là 3 cm; mặt đáy là có bán kính là 2 cm. Hãy tính
a) thể tích khối trụ
b) diện tích mặt đáy
Hướng dẫn giải
Đổi đơn vị
- h = 3 cm = 0,03 m
- r = 2 cm = 0,02 m
Áp dụng công thức $V = h.\pi .{r^2}$
a) Thể tích khối trụ: $V = \left( {0,03} \right).\pi .{\left( {0,02} \right)^2}$$V = \left( {0,03} \right).\pi .{\left( {0,02} \right)^2}$$ = 3,{768.10^{ – 5}}\left( {{m^2}} \right)$ (m3)
b) Diện tích mặt đáy được xác định theo công thức $S = \pi {r^2}$$S = \pi {r^2}$$ = \pi .{\left( {0,02} \right)^2}$$ = 1,{256.10^{ – 3}}\left( {{m^2}} \right)$ (m2)
Bài toán 2. Một khối trụ có thể tích 1(m3), đường cao 0,5m. Hãy tìm
a) bán kính măt đáy
b) Diện tích mặt đáy
c) chu vi đáy
d) diện tích xung quanh
Hướng dẫn giải
Áp dụng công thức $V = h.\pi .{r^2}$$ \Rightarrow r = \sqrt {\frac{V}{{h.\pi .}}} \left( * \right)$
a) Thay số vào (*) ta suy ra được bán kính mặt đáy: $r = \sqrt {\frac{1}{{0,5.\pi .}}} = 0,8\left( m \right)$
b) Vì mặt đáy có dạng hình trònn nên diện tích mặt đáy được xác định: $S = \pi {r^2}$$ = \pi .{\left( {0,8} \right)^2}$$ = 2,0096\left( {{m^2}} \right)$
c) Diện tích xung quanh được xác định theo S = 2π.r.h = 2π.0,8.0,5 = 2,512 (m2)
Bài viết này đã giúp bạn hiểu thêm được kiến thức hình khối trụ, một trong những hình thường gặp trong đời sống thực tế cũng như những bài toán xuất hiện trong đề thi.