Có khá nhiều cách để giải bt vật lý nhưng sử dụng phương pháp cơ năng con lắc dao động điều hòa là 1 cách hiệu quả được nhiều người dùng. Bài viết này sẽ giới thiệu với bạn từ cơ sở lý thuyết tới bài tập mình họa.
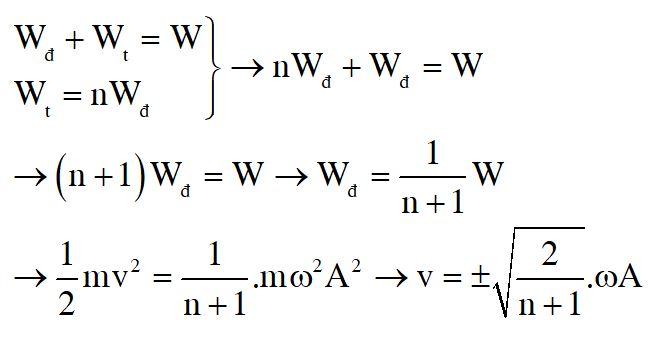
Mục lục
Cơ sở lý thuyết
Cơ năng con lắc là gì?
Cơ năng là dạng năng lượng của con lắc, trong dao động điều hòa thì nó luôn bằng tổng động năng và thế năng
Biểu thức tổng quát
\[{\rm{W}} = {W_t} + {W_d} = \frac{1}{2}k{x^2} + \frac{1}{2}m{v^2}\]
Từ biểu thức trên cho ta thấy cơ năng:
- bằng thế năng đàn hồi cực đại: $W = \frac{1}{2}k{A^2}$
- bằng động năng cực đại: $W = \frac{1}{2}m{\omega ^2}{A^2}$
Dựa vào các kiến thức trên, ta bắt đầu khảo sát:
Bài tập cơ năng con lắc
Câu 1. Cho chất điểm 1 con lắc đang dao động điều hòa với biên độ A và tần số góc ω. Hãy thiết lập công thức vận tốc khi biết thế năng gấp n lần động năng.
A. $ \pm \omega A\sqrt {\frac{2}{{n + 1}}} .$
B. $\omega A\sqrt {\frac{n}{{n + 1}}} .$
C. $ \pm \omega A\sqrt {\frac{{2n}}{{n + 1}}} .$
D. $ \pm \frac{1}{{\omega A}}\sqrt {\frac{n}{{n + 1}}} .$
Hướng dẫn trả lời
Theo biểu thức cơ năng con lắc thì ${W_d} + {W_t} = W$
Mặt khác, theo đề bài ${W_t} = n{W_d}$
Khi đó: $n{W_d} + {W_d} = W$
$ \to \left( {n + 1} \right){W_d} = W \to {W_d} = \frac{1}{{n + 1}}W$
$ \to \frac{1}{2}m{v^2} = \frac{1}{{n + 1}}.m{\omega ^2}{A^2}$
Kết quả là: $v = \pm \sqrt {\frac{2}{{n + 1}}} .\omega A$
Chọn đáp án: A.
Câu 2. Một chất điểm của con lắc được kích thích cho dao động điều hòa với biên độ A và tần số góc ω. Dựa vào bài 1, hãy xác định vận tốc của vật khi mà thế năng bằng 3 lần động năng?
A. ± 0,5ωA
B. 0,3333ωA
C. $\frac{{\sqrt 2 }}{3}$ωA
D. ±$\frac{{\sqrt 3 }}{2}$ωA
Hướng dẫn trả lời
Dựa theo công thức xây dựng được từ bài 1, ta có thể suy ra ngay biểu thức vận tốc con lắc $v = \pm \sqrt {\frac{{2n}}{{n + 1}}} .\omega A = \pm \sqrt {\frac{{2.\frac{1}{3}}}{{\frac{1}{3} + 1}}} .\omega A = \pm \frac{{\omega A}}{2}$
Chọn đáp án: A.
Câu 3. Nếu như một con lắc lò xo đang dao động điều hòa với biên độ A, tần số góc ω và biên độ A xác định. Hỏi rằng lúc động năng bằng 3 lần thế năng thì vận tốc có biểu thức nào trong các đáp án sau
A. $ \pm \frac{{\sqrt 6 }}{2}\omega A.$
B. $ \pm \frac{{\sqrt 3 }}{2}\omega A.$
C. $ \pm \frac{{\sqrt 2 }}{6}\omega A.$
D. $ \pm \frac{{\sqrt 2 }}{3}\omega A.$
Hướng dẫn trả lời
Áp dụng công thức tính cơ năng của con lắc vào xây dựng biểu thức thì theo ví dụ 1, ta rút ra được công thức vận tốc tổng quát: $v = \pm \sqrt {\frac{{2n}}{{n + 1}}} .\omega A$
Theo đề: ${W_t} = 3{W_d} \Rightarrow v = \pm \sqrt {\frac{{2.3}}{{3 + 1}}} .\omega A = \pm \frac{{\sqrt 6 }}{2}\omega A$
Chọn đáp án: A.
Dựa vào công thức cơ năng con lắc, ta đã giải nhanh tất cả các bài toán liên quan tới vận tốc. Đây là dạng bài hay