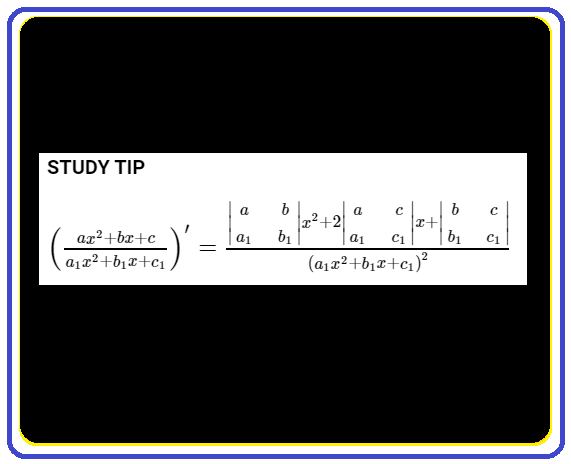
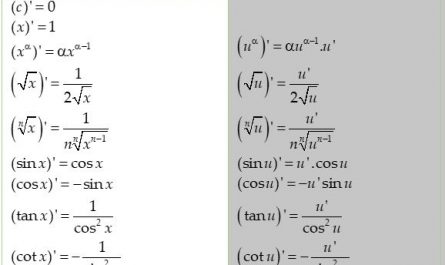Trong bảng công thức đạo hàm ta đã làm quen với đạo hàm lượng giác. Các công thức này không được luyện tập nhiều sẽ hay quên, nhất là sau thời gian dài không động tới. Bài này, ngoài nhắc lại công thức đạo hàm lượng giác còn cung cấp bài tập kèm lời giải chi tiết để học sinh học tập, ôn luyện hiệu quả hơn.
Mục lục
Cơ sở lý thuyết
Hàm cơ bản
- (sin x)’ = cos x
- (cos x)’ = – sin x
- $(tan x)’ = \frac{1}{{{{\cos }^2}x}}$
- $(cot x)’ = – \frac{1}{{{{\sin }^2}x}}$
Hàm hợp
- $(\sin u)’ = u’.\cos u$
- $(\cos u)’ = – u’\sin u$
- $\left( {\tan u} \right)’ = \frac{{u’}}{{{{\cos }^2}u}}$
- $\left( {\cot u} \right)’ = – \frac{{u’}}{{{{\sin }^2}u}}$
Bài tập vận dụng
Câu 1. Cho hàm số \(y = {\cot ^2}\frac{x}{4}\). Khi đó nghiệm của phương trình y’ = 0 là:
A. \(\pi + k2\pi \).
B. \(2\pi + k4\pi \).
C. \(2\pi + k\pi \).
D. \(\pi + k\pi \).
Lời hướng dẫn giải
Chọn B.
Ta có: \(\frac{1}{2}.\cos \sqrt {2 + {x^2}} .\)
\(\begin{array}{l}y’ = \left( {{{\cot }^2}\frac{x}{4}} \right)’\\ = 2\cot \frac{x}{4}\left( {\cot \frac{x}{4}} \right)’\\ = \frac{1}{2}\cot \frac{x}{4}\left( {1 + {{\cot }^2}\frac{x}{4}} \right)\end{array}\)
\(\begin{array}{l}y’ = 0 \Leftrightarrow \frac{1}{2}\cot \frac{x}{4}\left( {1 + {{\cot }^2}\frac{x}{4}} \right)\\ \Leftrightarrow \cot \frac{x}{4} = 0 \Leftrightarrow \frac{x}{4} = \frac{\pi }{2} + k\pi \\ \Leftrightarrow x = 2\pi + k4\pi ,\,\,k \in Z\end{array}\)
Câu 2. Tính đạo hàm của hàm số sau: \(y = \sin \sqrt {2 + {x^2}} \).
A. \(\cos \sqrt {2 + {x^2}} .\)
B. \(\frac{1}{{\sqrt {2 + {x^2}} }}.\cos \sqrt {2 + {x^2}} .\)
C. \(\cos \sqrt {2 – {x^2}} .\)
D. \(\frac{x}{{\sqrt {2 + {x^2}} }}.\cos \sqrt {2 + {x^2}} .\)
Lời hướng dẫn giải
Chọn D.
Áp dụng công thức \({\left( {\sin u} \right)^/}\) với \(u = \sqrt {2 + {x^2}} \)
\(\begin{array}{l}y’ = \cos \sqrt {2 + {x^2}} .{\left( {\sqrt {2 + {x^2}} } \right)^/}\\ = \cos \sqrt {2 + {x^2}} .\frac{{{{\left( {2 + {x^2}} \right)}^/}}}{{2\sqrt {2 + {x^2}} }}\\ = \frac{x}{{\sqrt {2 + {x^2}} }}.\cos \sqrt {2 + {x^2}} .\end{array}\)
Câu 3. Tính đạo hàm của hàm số sau: \(y = 2{\sin ^2}4x – 3{\cos ^3}5x\).
A. $y’ = \sin 8x + \frac{{45}}{2}cos5x.\sin 10x$
B. \(y’ = 8\sin 8x + \frac{5}{2}cos5x.\sin 10x\)
C. \(y’ = 8\sin x + \frac{{45}}{2}cos5x.\sin 10x\)
D. \(y’ = 8\sin 8x + \frac{{45}}{2}cos5x.\sin 10x\)
Lời hướng dẫn giải
Chọn D.
Bước đầu tiên áp dụng \({\left( {u + v} \right)^/}\)
\(y’ = {\left( {2{{\sin }^2}4x} \right)^/} – 3{\left( {{{\cos }^3}5x} \right)^/}\)
Tính \({\left( {{{\sin }^2}4x} \right)^/}\): Áp dụng \({\left( {{u^\alpha }} \right)^/}\), với \(u = \sin 4x,\) ta được:
\({\left( {{{\sin }^2}4x} \right)^/} = 2\sin 4x.{\left( {\sin 4x} \right)^/} = 2\sin 4x.\cos 4x{\left( {4x} \right)^/} = 4\sin 8x.\)
Tương tự: \({\left( {{{\cos }^3}5x} \right)^/} = 3{\cos ^2}5x.{\left( {\cos 5x} \right)^/} = 3{\cos ^2}5x.\left( { – \sin 5x} \right).{\left( {5x} \right)^/}\)
\( = – 15{\cos ^2}5x.\sin 5x = \frac{{ – 15}}{2}cos5x.\sin 10x.\)
Kết luận: \(y’ = 8\sin 8x + \frac{{45}}{2}cos5x.\sin 10x\)
Câu 4. Tính đạo hàm của hàm số sau: \(y = {\sin ^3}2x.{\cos ^3}2x\)
A. \({\sin ^2}4x.\cos 4x.\)
B. \(\frac{3}{2}{\sin ^2}x.\cos x.\)
C. \({\sin ^2}x.\cos 4x.\)
D. \(\frac{3}{2}{\sin ^2}4x.\cos 4x.\)
Lời hướng dẫn giải
Chọn D.
\(\begin{array}{l}y = {\sin ^3}2x.{\cos ^3}2x\\ = {\left( {\sin 2x.\cos 2x} \right)^3}\\ = {\left( {\frac{1}{2}\sin 4x} \right)^3} = \frac{1}{8}.{\sin ^3}4x\end{array}\)
Áp dụng \({\left( {{u^\alpha }} \right)^/},u = \sin 4x.\)
\(\begin{array}{l}y’ = \frac{1}{8}.3{\sin ^2}4x\left( {\sin 4x} \right)’\\ = \frac{1}{8}.3{\sin ^2}4x.\cos 4x.\left( {4x} \right)’\\ = \frac{3}{2}{\sin ^2}4x.\cos 4x.\end{array}\)
Câu 5. Cho hàm số \(y = f(x) – {\cos ^2}x\) với $f\left( x \right)$ là hàm liên tục trên R. Trong bốn biểu thức dưới đây, biểu thức nào xác định hàm $f\left( x \right)$ thỏa mãn $y’ = 1$ với mọi \(x \in R\)?
A. $x + \frac{1}{2}\cos 2x$.
B. \(x – \frac{1}{2}\cos 2x\).
C. x – sin 2x.
D. x + sin 2x.
Lời hướng dẫn giải
Chọn A.
\(\begin{array}{l}y’ = f’\left( x \right) – 2.\cos x.\left( { – \sin x} \right)\\ = f’\left( x \right) + 2.\cos x.\sin x\\ = f’\left( x \right) + \sin 2x\end{array}\)
\(\begin{array}{l} \Rightarrow y’ = 1\\ \Leftrightarrow f’\left( x \right) + \sin 2x = 1\\ \Leftrightarrow f’\left( x \right) = 1 – \sin 2x\\ \Leftrightarrow f\left( x \right) = x + \frac{1}{2}\cos 2x\end{array}\)
Câu 6. Hàm số \(y = \frac{{\cos x}}{{2{{\sin }^2}x}}\) có đạo hàm bằng:
A. \( – \frac{{1 + {{\sin }^2}x}}{{2{{\sin }^3}x}}\).
B. \( – \frac{{1 + {{\cos }^2}x}}{{2{{\sin }^3}x}}\).
C. \(\frac{{1 + {{\sin }^2}x}}{{2{{\sin }^3}x}}\).
D. \(\frac{{1 + {{\cos }^2}x}}{{2{{\sin }^3}x}}\).
Lời hướng dẫn giải
Chọn B.
Ta có:
\(\begin{array}{l}y’ = \left( {\frac{{\cos x}}{{2{{\sin }^2}x}}} \right)’\\ = \frac{{{{\sin }^2}x\left( {\cos x} \right)’ – \left( {{{\sin }^2}x} \right)\cos x}}{{2{{\sin }^4}x}}\\ = \frac{{ – {{\sin }^3}x – 2\sin x\cos x\cos x}}{{2{{\sin }^4}x}}\end{array}\)
\( = – \frac{{{{\sin }^2}x + 2{\rm{co}}{{\rm{s}}^2}x}}{{{{\sin }^3}x}} = – \frac{{1 + {\rm{co}}{{\rm{s}}^2}x}}{{{{\sin }^3}x}}\)
Câu 7. Tính đạo hàm của hàm số sau \(y = {\sin ^2}(3x + 1)\)
A. \(3\sin (6x + 2)\)
B. \(\sin (6x + 2)\)
C. \( – 3\sin (6x + 2)\)
D. \(3\cos (6x + 2)\)
Lời hướng dẫn giải
Chọn D.
Ta có:
\(\begin{array}{l}y’ = 2\sin (3x + 1).\left[ {\sin (3x + 1)} \right]’\\ = 2\sin (3x + 1).3\cos (3x + 1)\\ = 3\sin (6x + 2)\end{array}\).
Câu 8. Tính đạo hàm của hàm số sau: \(y = \frac{1}{{{{\cos }^2}x – {{\sin }^2}x}} = \frac{1}{{\cos 2x}}\).
A. \(\frac{{\sin 2x}}{{{{\cos }^2}2x}}.\)
B. \(\frac{{\sin x}}{{{{\cos }^2}2x}}.\)
C. $\frac{{2\cos 2x}}{{{{\sin }^2}2x}}.$
D. \(\frac{{2\sin 2x}}{{{{\cos }^2}2x}}.\)
Lời hướng dẫn giải
Chọn D.
Áp dụng \({\left( {\frac{1}{u}} \right)^/}\).
\(y’ = \frac{{ – {{\left( {\cos 2x} \right)}^/}}}{{{{\left( {\cos 2x} \right)}^2}}} = \frac{{\sin 2x.{{\left( {2x} \right)}^/}}}{{{{\cos }^2}2x}} = \frac{{2\sin 2x}}{{{{\cos }^2}2x}}.\)
Câu 9. Cho hàm số $y = f(x) = \left\{ \begin{array}{l}\sin x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} & {\rm{khi}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x \ge 0\\\sin \left( { – x} \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} & {\rm{khi}}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x < 0\end{array} \right.$. Tìm khẳng định SAI?
A. Hàm số f không có đạo hàm tại ${x_0} = 0$.
B. Hàm số f không liên tục tại ${x_0} = 0$.
C. $f’\left( {\frac{\pi }{2}} \right) = 0$.
D. $f\left( {\frac{\pi }{2}} \right) = 1$.
Lời hướng dẫn giải
Chọn B.
Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \sin x = \sin 0 = 0\\\mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} \sin ( – x) = \sin 0 = 0\end{array} \right.\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to 0} f(x) = 0 = f(0)\)
\( \Rightarrow \) Hàm số liên tục tại \({x_0} = 0\)
Câu 10. Tính đạo hàm của hàm số sau \(f(x) = \left\{ \begin{array}{l}{x^3}\sin \frac{1}{x}{\rm{ khi }}x \ne 0\\0{\rm{ khi }}x = 0{\rm{ }}\end{array} \right.\)
A. \(f'(x) = \left\{ \begin{array}{l}{x^2}\sin \frac{1}{x} – x\cos \frac{1}{x}{\rm{ khi }}x \ne 0\\{\rm{0 khi }}x = 0\end{array} \right.\)
B. \(f'(x) = \left\{ \begin{array}{l}3{x^2}\sin \frac{1}{x} – x\cos \frac{1}{x}{\rm{ khi }}x \ne 0\\0{\rm{ khi }}x = 0\end{array} \right.\)
C. \(f'(x) = \left\{ \begin{array}{l}3{x^2}\sin \frac{1}{x} + x\cos \frac{1}{x}{\rm{ khi }}x \ne 0\\0{\rm{ khi }}x = 0\end{array} \right.\)
D. \(f'(x) = \left\{ \begin{array}{l}3{x^2}\sin \frac{1}{x} – \cos \frac{1}{x}{\rm{ khi }}x \ne 0\\0{\rm{ khi }}x = 0\end{array} \right.\)
Lời hướng dẫn giải
Chọn D.
\(x \ne 0 \Rightarrow f'(x) = 3{x^2}\sin \frac{1}{x} – x\cos \frac{1}{x}\)
Với \(x = 0 \Rightarrow f'(0) = \mathop {\lim }\limits_{x \to 0} \frac{{f(x) – f(0)}}{x} = 0\)
Vậy \(f'(x) = \left\{ \begin{array}{l}3{x^2}\sin \frac{1}{x} – x\cos \frac{1}{x}{\rm{ khi }}x \ne 0\\0{\rm{ khi }}x = 0\end{array} \right.\).
Hy vọng với bài viết này sẽ giúp ích em học tập hiệu quả!